ERF_RichardsonNumber.H File Reference

#include <AMReX_GpuQualifiers.H>
#include <AMReX_REAL.H>
#include <cmath>
#include "ERF_Constants.H"
#include "ERF_IndexDefines.H"
#include "ERF_DataStruct.H"
#include "ERF_MoistUtils.H"

Include dependency graph for ERF_RichardsonNumber.H:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
AMREX_GPU_DEVICE AMREX_FORCE_INLINE bool	IsSaturated (int i, int j, int k, const amrex::Array4< const amrex::Real > &cell_data, int qc_index)
AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real	ComputeN2 (int i, int j, int k, amrex::Real dzInv, amrex::Real const_grav, const amrex::Array4< const amrex::Real > &cell_data, const MoistureComponentIndices &moisture_indices)
AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real	ComputeVerticalShear2 (int i, int j, int k, amrex::Real dzInv, const amrex::Array4< const amrex::Real > &u, const amrex::Array4< const amrex::Real > &v)
AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real	ComputeRichardson (amrex::Real N2_moist, amrex::Real S2_vert)
AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real	StabilityFunction (amrex::Real Ri, amrex::Real Ri_crit)

Detailed Description

Functions for computing moist Richardson number and Mason (1989) stability function for Smagorinsky turbulence closure with conditional instability correction.

PHYSICAL BACKGROUND:

In cloud-resolving simulations, standard Smagorinsky models overpredict turbulent mixing in conditionally unstable regions (cloud updrafts) where buoyancy-driven instability occurs. This module implements the moist Richardson number correction following Mason (1989) and Stevens et al. (2005) for marine stratocumulus.

KEY EQUATIONS:

1. Moist Brunt-Väisälä frequency: N²_moist = (g/θ_v) * ∂θ_v/∂z (unsaturated) N²_moist = (g/θ_l) * ∂θ_l/∂z (saturated, in clouds)
2. Moist Richardson number: Ri_moist = N²_moist / S²_vert where S²_vert = (∂u/∂z)² + (∂v/∂z)²
3. Mason (1989) stability function: f(Ri) = 0 if Ri ≥ Ri_crit (complete suppression) = sqrt(1 - Ri/Ri_crit) if 0 < Ri < Ri_crit (partial suppression) = 1 if Ri ≤ 0 (no suppression, unstable/neutral)
4. Corrected vertical eddy viscosity: μ_t,v = ρ(C_s·Δ)²|S| · f(Ri_moist)

PHYSICAL INTERPRETATION:

• In cloud updrafts: ∂θ_l/∂z < 0 → Ri < 0 → f(Ri) = 1.0 → full mixing (correct!)
• In stable regions: ∂θ_v/∂z > 0 → Ri > 0 → f(Ri) < 1.0 → reduced mixing
• In neutral regions: Ri ≈ 0 → f(Ri) ≈ 1.0 → standard Smagorinsky

CUDA-CONSERVATIVE DESIGN:

• All functions are explicit device functions (not lambdas)
• Use simple scalar parameters (no struct captures in device context)
• Geometry passed via local scalars (dzInv), not complex objects
• Reuse existing ERF GetThetav/GetThetal from ERF_MoistUtils.H

REFERENCES:

• Mason, P. J. (1989): Large-eddy simulation of the convective atmospheric boundary layer. J. Atmos. Sci., 46, 1492-1516.
• Stevens et al. (2005): Evaluation of large-eddy simulations via observations of nocturnal marine stratocumulus. Mon. Wea. Rev., 133, 1443-1462.
• Smagorinsky, J. (1963): General circulation experiments with the primitive equations. Mon. Wea. Rev., 91, 99-164.

Function Documentation

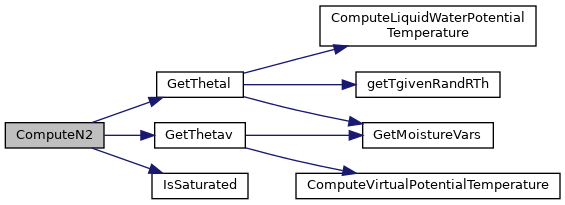
ComputeN2()

AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real ComputeN2	(	int	i,
		int	j,
		int	k,
		amrex::Real	dzInv,
		amrex::Real	const_grav,
		const amrex::Array4< const amrex::Real > &	cell_data,
		const MoistureComponentIndices &	moisture_indices
	)

Compute moist Brunt-Väisälä frequency squared (N²_moist).

Parameters

[in]	i,j,k	cell indices
[in]	dzInv	inverse vertical grid spacing (1/Δz) [1/m]
[in]	const_grav	gravitational acceleration g [m/s²]
[in]	cell_data	conserved state
[in]	moisture_indices	moisture species indices

Returns

N²_moist [1/s²]

PHYSICS:

Uses centered finite differences: ∂/∂z ≈ (f_{k+1} - f_{k-1}) / (2Δz)

Unsaturated: N² = (g/θ_v) · ∂θ_v/∂z where θ_v = θ(1 + 0.61q_v - q_c) accounts for vapor buoyancy and condensate loading

Saturated: N² = (g/θ_l) · ∂θ_l/∂z where θ_l = θ - (L_v/c_p·Π)·q_c is the liquid water potential temperature

CONDITIONAL INSTABILITY:

In cloud updrafts, ∂θ_l/∂z can be negative due to release of latent heat during ascent. This gives N² < 0, which is physically correct for convective instability and should enhance (not suppress) mixing.

UNITS:

Input: dzInv [1/m], const_grav [m/s²], θ [K] Output: N² [1/s²]

{
    const int rho_comp       = Rho_comp;
    const int rhoTheta_comp  = RhoTheta_comp;
    const int qv_index = moisture_indices.qv;
    const int qc_index = moisture_indices.qc;
 
    amrex::Real rho = cell_data(i, j, k, rho_comp);
 
    bool saturated = IsSaturated(i, j, k, cell_data, qc_index);
 
    amrex::Real inv_theta;
    amrex::Real dtheta_dz;
 
    if (saturated && qc_index >= 0) {
        amrex::Real theta_l    = GetThetal(i, j, k  , cell_data, moisture_indices);
        amrex::Real theta_l_kp1= GetThetal(i, j, k+1, cell_data, moisture_indices);
        amrex::Real theta_l_km1= GetThetal(i, j, k-1, cell_data, moisture_indices);
 
        inv_theta = 1.0 / theta_l;
        dtheta_dz = 0.5 * (theta_l_kp1 - theta_l_km1) * dzInv;
 
    } else if (qv_index >= 0) {
        amrex::Real theta_v    = GetThetav(i, j, k  , cell_data, moisture_indices);
        amrex::Real theta_v_kp1= GetThetav(i, j, k+1, cell_data, moisture_indices);
        amrex::Real theta_v_km1= GetThetav(i, j, k-1, cell_data, moisture_indices);
 
        inv_theta = 1.0 / theta_v;
        dtheta_dz = 0.5 * (theta_v_kp1 - theta_v_km1) * dzInv;
 
    } else {
        amrex::Real theta = cell_data(i, j, k, rhoTheta_comp) / rho;
        amrex::Real theta_kp1 = cell_data(i, j, k+1, rhoTheta_comp) / cell_data(i, j, k+1, rho_comp);
        amrex::Real theta_km1 = cell_data(i, j, k-1, rhoTheta_comp) / cell_data(i, j, k-1, rho_comp);
 
        inv_theta = 1.0 / theta;
        dtheta_dz = 0.5 * (theta_kp1 - theta_km1) * dzInv;
    }
 
    return const_grav * inv_theta * dtheta_dz;
}

Referenced by ComputeTurbulentViscosityLES().

Here is the call graph for this function:

Here is the caller graph for this function:

ComputeRichardson()

AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real ComputeRichardson	(	amrex::Real	N2_moist,
		amrex::Real	S2_vert
	)

Compute moist Richardson number.

Parameters

[in]	N2_moist	moist Brunt-Väisälä frequency squared [1/s²]
[in]	S2_vert	vertical wind shear squared [1/s²]

Returns

Ri_moist = N²_moist / S²_vert [dimensionless]

{
    amrex::Real S2_safe = amrex::max(S2_vert, 1.0e-10);
    return N2_moist / S2_safe;
}

Referenced by ComputeTurbulentViscosityLES().

Here is the caller graph for this function:

ComputeVerticalShear2()

AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real ComputeVerticalShear2	(	int	i,
		int	j,
		int	k,
		amrex::Real	dzInv,
		const amrex::Array4< const amrex::Real > &	u,
		const amrex::Array4< const amrex::Real > &	v
	)

Compute vertical shear squared (S²_vert).

Parameters

[in]	i,j,k	cell indices
[in]	dzInv	inverse vertical grid spacing (1/Δz) [1/m]
[in]	u	face-centered x-velocity (u) array with ngrow≥1 in z
[in]	v	face-centered y-velocity (v) array with ngrow≥1 in z

Returns

S²_vert = (∂u/∂z)² + (∂v/∂z)² [1/s²]

DISCRETIZATION:

ERF uses Arakawa C-grid: u defined at (i+1/2, j, k) (x-faces) v defined at (i, j+1/2, k) (y-faces) w defined at (i, j, k+1/2) (z-faces) cell centers at (i, j, k)

To get shear at cell center (i,j,k), interpolate velocities to center then difference: ∂u/∂z|_{i,j,k} ≈ (u_{i,j,k+1} - u_{i,j,k-1}) / (2Δz) where u_{i,j,k} = 0.5 * (u_{i-1/2,j,k} + u_{i+1/2,j,k})

UNITS:

Input: dzInv [1/m], u, v [m/s] Output: S²_vert [1/s²]

{
    amrex::Real u_c_km1 = 0.5 * (u(i, j, k-1) + u(i+1, j, k-1));
    amrex::Real u_c_kp1 = 0.5 * (u(i, j, k+1) + u(i+1, j, k+1));
 
    amrex::Real v_c_km1 = 0.5 * (v(i, j, k-1) + v(i, j+1, k-1));
    amrex::Real v_c_kp1 = 0.5 * (v(i, j, k+1) + v(i, j+1, k+1));
 
    amrex::Real du_dz = 0.5 * (u_c_kp1 - u_c_km1) * dzInv;
    amrex::Real dv_dz = 0.5 * (v_c_kp1 - v_c_km1) * dzInv;
 
    amrex::Real S2_vert = du_dz * du_dz + dv_dz * dv_dz;
 
    return S2_vert;
}

Referenced by ComputeTurbulentViscosityLES().

Here is the caller graph for this function:

IsSaturated()

AMREX_GPU_DEVICE AMREX_FORCE_INLINE bool IsSaturated	(	int	i,
		int	j,
		int	k,
		const amrex::Array4< const amrex::Real > &	cell_data,
		int	qc_index
	)

Check if grid cell is saturated based on cloud liquid water content.

Parameters

[in]	i,j,k	cell indices
[in]	cell_data	conserved state (ρ, ρθ, ρq_v, ρq_c, etc.)
[in]	moisture_indices	indices for moisture species

Returns

true if saturated (q_c > 1e-8 kg/kg), false otherwise

PHYSICAL JUSTIFICATION: Threshold of 1e-8 kg/kg (0.01 g/kg) is typical for distinguishing cloudy from clear regions in LES. Below this threshold, condensate is negligible and air is effectively unsaturated.

{
    if (qc_index >= 0) {
        amrex::Real rho = cell_data(i, j, k, Rho_comp);
        amrex::Real qc = cell_data(i, j, k, qc_index) / rho;
        return (qc > 1.0e-8);  // 0.01 g/kg threshold
    }
    return false;
}

Referenced by ComputeN2().

Here is the caller graph for this function:

StabilityFunction()

AMREX_GPU_DEVICE AMREX_FORCE_INLINE amrex::Real StabilityFunction	(	amrex::Real	Ri,
		amrex::Real	Ri_crit
	)

Mason (1989) stability function for turbulent mixing suppression.

Parameters

[in]	Ri	gradient Richardson number [dimensionless]
[in]	Ri_crit	critical Richardson number (default 0.25)

Returns

f(Ri) ∈ [0, 1] [dimensionless]

{
    if (Ri >= Ri_crit) {
        return 0.0;
    } else if (Ri > 0.0) {
        return std::sqrt(1.0 - Ri / Ri_crit);
    } else {
        return 1.0;
    }
}

Referenced by ComputeTurbulentViscosityLES().

Here is the caller graph for this function: